Mathematik ist eine der ältesten Wissenschaften der Welt und eine der umfangreichsten. Sie gilt zudem als Hilfswissenschaft für viele andere Wissenschaften. Die Mathematik wird bereits in der Schule gelehrt und gilt als Grundlage des Allgemeinwissens. Doch die Mathematik besteht aus einer Vielzahl von Teilgebieten, die sich erst im Lauf der Geschichte entwickelt haben.

Zahlen und Geometrie

Mathematische Algorithmen spielten bereits in der Antike eine Rolle. Zahlen und Zahlensysteme bildeten die Grundlage für den Handel, und die Geometrie war eine Voraussetzung für den Bau von Gebäuden und Pyramiden. Die euklidische Geometrie beschreibt die geometrischen Verhältnisse im zwei- und dreidimensionalen Raum. Sie ist noch heute die bekannteste Form der Geometrie. Darüber hinaus gibt es Teilgebiete, die sich mit der analytischen Geometrie oder der Topologie beschäftigen.

Auch bei den Zahlen gibt es bestimmte mathematische Differenzierungen. Am bekanntesten ist die Arithmetik. In der Arithmetik setzt man sich mit dem Zählen und dem Rechnen mit natürlichen Zahlen auseinander. Dazu gehören auch die Grundrechenarten wie Addition, Subtraktion, Division und Multiplikation. Daneben gibt es die Zahlentheorie, die sich mit der Teilbarkeit von Zahlen beschäftigt.

Gleichungen und Logik

Zur Mathematik gehören auch das Lösen von Gleichungen und die Logik. Ersteres wird in der Algebra behandelt. Algebraische Rechenoperationen dienen oft als mathematische Beweise für aufgestellte physikalische oder ökonomische Theorien. Gleichungen bilden einen wesentlichen Bestandteil bekannter Wirtschaftstheorien. Die berühmteste Gleichung E = mc² von Albert Einstein bildete die Grundlage für die Atombombe. Allerdings 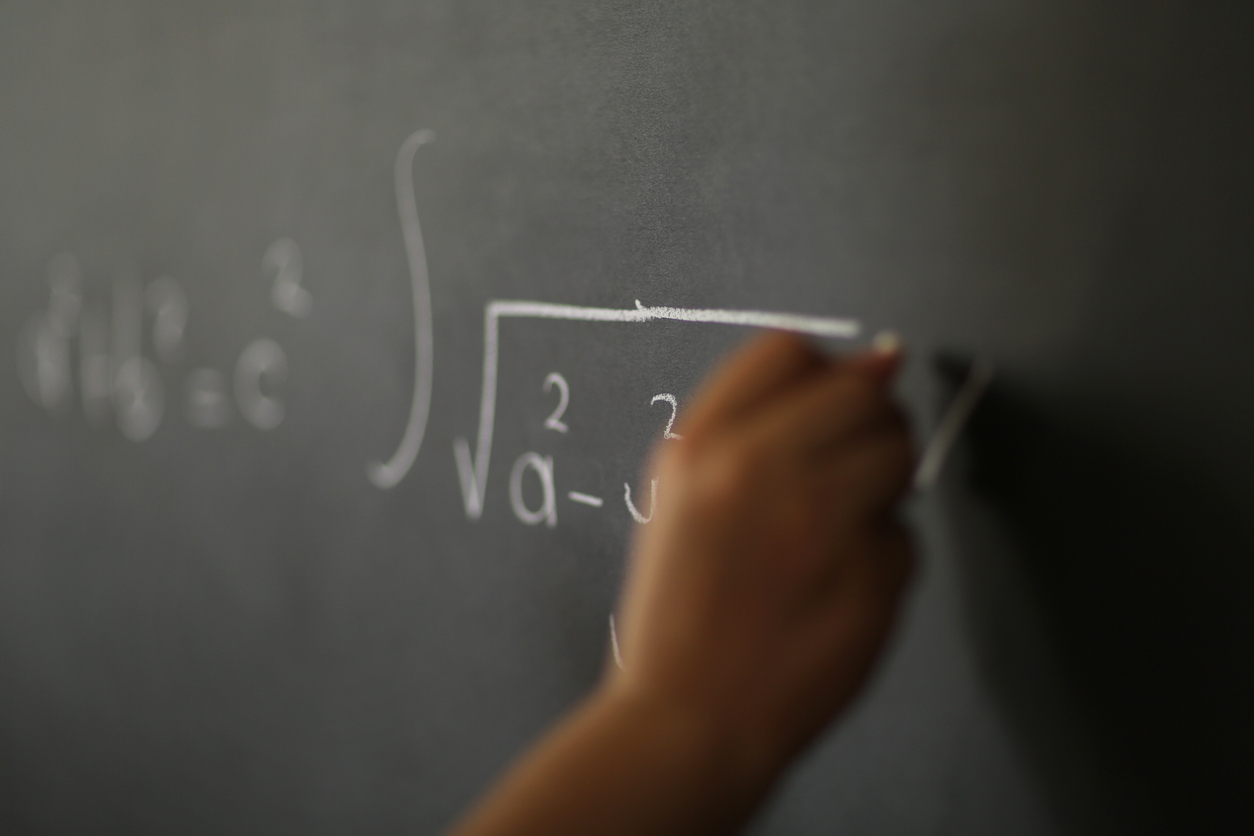war dies eine unbeabsichtigte Folge seiner mathematischen Entdeckung. Doch auch in der Astronomie spielt diese Gleichung eine wesentliche Rolle. Die Tatsache, dass die Lichtgeschwindigkeit die höchste mögliche Geschwindigkeit darstellt, geht auf diese Gleichung zurück. Ferner ist auch die Logik ein Teilgebiet der Mathematik. Sie beschreibt die Fähigkeit, aus bestimmten Gegebenheiten korrekte Schlussfolgerungen zu ziehen.

Andere mathematische Teilgebiete

Zu weiteren Teilbereichen der Mathematik zählen beispielsweise:

• Die Wahrscheinlichkeitsrechnung: Sie beschreibt die Wahrscheinlichkeit des Eintretens eines bestimmten Ereignisses und versieht diese mit einem Zahlenwert. Meist wird dieser in Prozent ausgedrückt. Die Wahrscheinlichkeitsrechnung ist vor allem in der Spieltheorie sowie in der Versicherungsmathematik von Bedeutung.
• Die Mengenlehre: Dieser Teilbereich befasst sich mit der Zusammenfassung von Objekten in einer Menge. Die Mengenlehre bildet die Grundlage für fast alle mathematischen Operationen. Die gesamte Mathematik baut auf den Erkenntnissen der Mengenlehre auf.
• Die Statistik: Sie analysiert als mathematische Wissenschaft die Häufigkeit einer Verteilung von bestimmten Ereignissen. Die Statistik wird in der Wirtschaftsmathematik angewandt, aber auch in der Medizin und Pharmazie.

Daneben gibt es noch eine Vielzahl anderer mathematischer Teilgebiete, die sich mit Zahlen, der Geometrie oder verschiedenen Verhältnissen von bestimmten Fakten zueinander auseinandersetzen. Die Mathematik bildet also eine sehr umfangreiche Wissenschaft und ist Ausgangsbasis für viele andere wissenschaftliche Disziplinen. Die Welt baut auf der Mathematik auf, auch wenn manche das gern anders sehen.